14. How Lists Work
How Lists Work
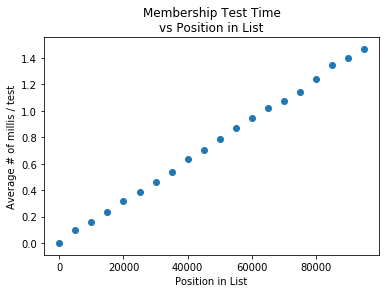
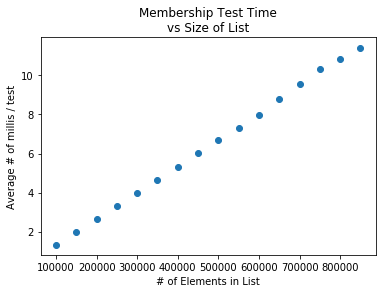
In the previous section you saw two graphs that looked something like these:
SOLUTION:
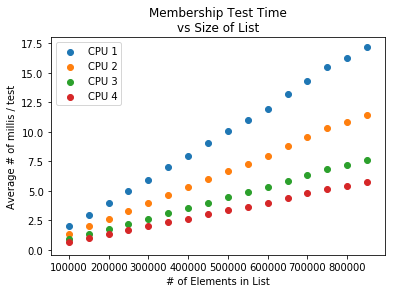
10 millisecondsWe repeated the second experiment on 4 different computers, each of which had a different processor. The results of this experiment are shown below.
SOLUTION:
CPU 4SOLUTION:
The time it takes to scan a list of 800,000 elements is about **twice** the amount of time it takes to scan a list with 400,000 elements.SOLUTION:
about 1 msHow do lists work?
The time it takes to test for membership in a list "scales linearly" with the size of the list. That just means if you double the size of the list you double the amount of time it takes to test for membership of an element (on average).
Note: As you learn more, you might see this algorithm described as "big O of N", or mathematically as \mathcal{O}(n). We aren't going to get too deep into the topic at this time, but this notation is all about the analysis of algorithms in relation to their efficiency.
The reason it takes longer to membership test a big list has to do with what the computer is doing behind the scenes. When you write:
if -1 in my_list
The computer will go through every single element of my_list in order until it finds -1. If it makes it through the entire list without finding -1 then the result of the membership test will be False.